約数と素数に関する問題です。
約数、素数の言葉の意味 公約数、最大公約数の求め方は小学校5年生で習います。まだ学校で習っていなくて、基本的な言葉の意味がよく分からない場合は、塾の教材だけでなく5年生向けの教材で学習してください。
約数や素数の基本レベルの問題は無料で使える学習ドリルにあります。
また中学受験レベルでよく出題されるのは
整数を素数の積に分解する 約数の個数のもとめ方などです。
整数を素数の積に分解する
12=2×2×3
24=2×2×2×3
のように、整数を素数の積で表します。
12や24くらいの数なら、少し考えれば出来ると思いますが、数が大きくなると混乱していきます。
中学の素因数分解で習う素数でわっていく方法を覚えておいた方がいいでしょう。
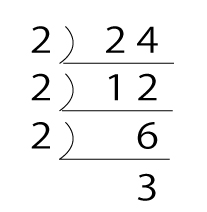
24=2×2×2×3
約数の個数のもとめ方
24の約数の個数をもとめなさい
という問題が出ます。
このくらいなら約数を全部書いて数えても時間はそんなにかからないと思います。
実際に書いてみると
1 2 3 4 6 8 12 24
の8個ですね。(212)(3×8) (4×6) というようにかけて24になる対になる組み合わせをしっかり確認して、飛ばさないように書き出してください。
しかし、
360の約数の個数を求めなさい
という問題が出てきたら、書き出して数えるのが大変になります。
そこで、さきほどの素因数分解を使って出す方法が公式として覚えるように塾で習うと思います。
![]()
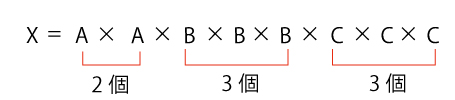
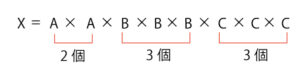
例) 108=2×2×3×3×3
108は2が 2個 と 3が 3個 の 積
約数の個数=(2+1)× (3+1)=12 よって約数の個数は12個になる。
これを丸暗記してしまえばいいのですが、最近の入試の傾向では、テキストに出てくる公式を丸暗記するだけでは解けない問題が増えています。
どうしてこうなるのかが説明出来るような学習をしてください。
24=2×2×2×3 の場合 約数の個数は 2が3個 3が1個なので(3+1)×(1+1)=8個
約数を素数のかけ算で考えてみましょう。
24の約数は
1 1×2 1×3 1×2×2 1×2×3 1×2×2 1×2×2×3 1×2×2×3 になります。
これを表にすると
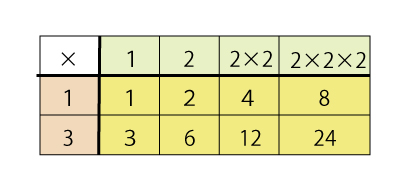
黄色の中が約数になるので、4通り×2通りになることがわかります。
面積で考えるなど、いろいろな考え方があるので、余裕があれば考えてみるようにしてください。
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロード出来ます。
|
中学入試算数よく出る場合の数60題 (難関中合格シリーズ 単元別対策 4) 新品価格 |
 |
![]()