時計算の問題です。
長針と短針が重なる時刻や一直線になる時刻を求めます。
解き方をしっかり理解していろいろな問題を解くようにしましょう。
長針と短針が重なる時刻
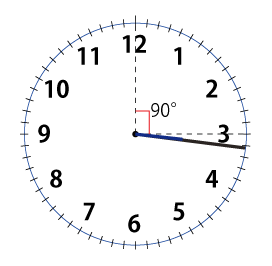
例)3時と4時の間で長針と短針が重なるのは何時何分ですか。
3時の時の長針と短針の角度は90°
長針と短針は1分間で5.5°ずつ縮まる。

長針と短針が一直線になる時刻
例)3時と4時の間で長針と短針が一直線になるのは何時何分ですか。
3時の時の長針と短針の角度は90°

長針と短針が一直線になるのは 長針が短針に追いついてから差が広がるから 90+180=270°
[math]270\div 5.5=270\times \frac { 2 }{ 11 } =\frac { 540 }{ 11 } =49\frac { 1 }{ 11 }[/math] [math]49\frac {1 }{ 11 }[/math]分例)10時と11時の間で長針と短針が一直線になるのは何時何分ですか。
9時の時の長針と短針の角度は300°
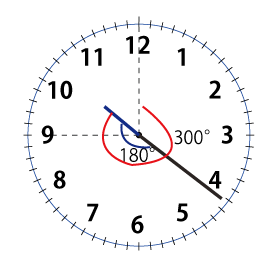
長針と短針が一直線になるのは 長針と短針がさらに180°縮まる
300-180=120°
[math]120\div 5.5=120\times \frac { 2 }{ 11 } =\frac {240 }{ 11 } =21\frac { 9}{ 11 }[/math] [math]21\frac {9}{ 11 }[/math]分練習問題をダウンロード
画像をクリックするとPDFファイルをダウンロード出来ます。
問題は追加する予定です。
|
時計算―中学入試問題をわかりやすくマンガで攻略 (マンガで算数シリーズ (4)) 新品価格 |
 |
![]()