時計算の問題です。
時計算は、時計の長針、短針が作り角度を距離とした旅人算で考えます。
速さの応用問題になりますが、やり方を身につけていないと難しく感じることが多くなります。
初めは時計を書きながら考えていくようにしましょう。
時計の長針、短針が１分間に進む角度を計算できるようにしておく
次のことは計算で求められますが、テスト前には覚えてしまうようにしてください。
長針は１時間に360°進む→ １分間に 360÷60＝6°進む
短針は12時間に360°進む→１時間に 360÷12＝30°進む
→１分間に 30÷60＝0.5°進む
ある時刻の短針と長針の角度の求め方
図を書いて角度を求める方法と、旅人算で考える方法があります。
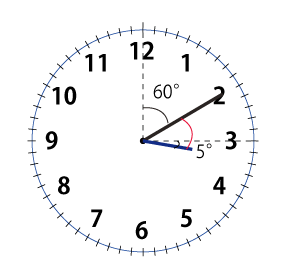
例１）3時１０分の時の長針と短針の小さい方の角度を求める
考え方１
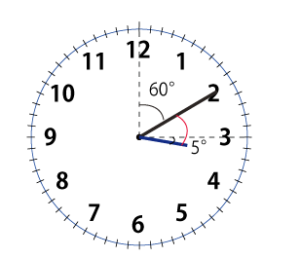３時の時の角度を基準に考える。
3時の時は 30×3＝90°
10分で
長針は 6×10＝60° 短針は 0.5×10＝5° 進む
図より、小さい方の角度を求めると 90-60+5＝35°
考え方2 旅人算で考える
長針と短針の速さの差は 6-0.5=5.5°
3時の時点から毎分5.5°ずつ縮まるので 90-5.5×10=35°
例２）3時１０分の時の長針と短針の小さい方の角度を求める
考え方１
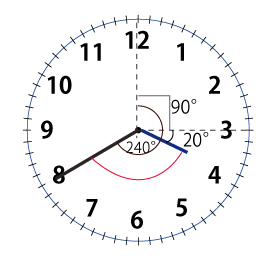３時の時の角度を基準に考える。
3時の時は 30×3＝90°
40分で
長針は 6×40＝240° 短針は 0.5×40＝20° 進む
図より、小さい方の角度を求めると 240-90-20＝130°
考え方2 旅人算で考える
長針と短針の速さの差は 6-0.5=5.5°
3時の時点から長針は短針を追い越して広がる 5.5×40-90=130°
＊慣れないうちは、時計を書いて考えるようにしてください。時計の作図を素早く出来るようにすることも大切です。
円をうまく書けない場合は、外側の円を書かないで時計の針だけの作図をするようにしましょう。
練習問題をダウンロード
画像をクリックするとPDFファイルをダウンロード出来ます。
＊解き方は解答例にこだわらないで、素早く解ける方法を自分で身につけるようにしてください。
→時計算基本２ （長針と短針が重なる時刻など）
