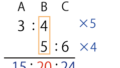逆比の問題です。
逆比という言葉で比を逆にすればいいという考え方で覚えてしまうと、3つ以上の連比で間違えてしまう事が多くなります。
まずは、文章題などで逆比の意味を理解するようにしましょう。
逆比の考え方
例1)Aの2倍とBの3倍が等しいとき、A:Bを求めなさい。
考え方1
A×2 と B×3 が等しくなるので、2と3の最小公倍数6を考えると
A×2=6
B×3=6
と考えられます。 よって A:B=3:2となります。 これが2:3の逆比となります。
考え方2
A×2=1
B×3=1
と考えると A=1/2 B=1/3
となり、A:B=1/2:1/3 となります。 これを簡単にすると A:B=3:2 となります。
逆比は 逆数の比になります。
分数の逆比を求める問題が出されたら、逆数の比を作って考えるようにしてください。
例2)Aの2倍とBの3倍とCの4倍が等しいとき、A:B:Cを求めなさい。
最小公倍数で考えると
A×2=12
B×3=12
C×4=12
なので A:B:C =6:4 :3
となります。
全体が1で考えると
A×2=1
B×3=1
C×4=1
A:B :C=1/2:1/3 :1/4 ←逆数の比
となり通分して簡単にすると A:B:C =6:4 :3 となります。
逆比を使った問題
かけて一定の値になるものが問題で出題されます。
- 面積が同じ長方形の縦と横の長さ
- 距離が同じ場合の速さとかかる時間
- 歯車の歯数と回転数
など
逆比を使えるいろいろな問題を解いて考え方を身につけるようにしてください。
*反比例の考え方でも解けるものもあります。いろいろな考え方ができるようにしていきましょう。
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロードできます。
*計算方法や解き方は解答例以外の解き方でも構いません。早くできる方法で解くようにしてください。