グラフをみて、旅人算の考え方を使う問題です。
2つのグラフが交わるところが、出会うところと追いつくところだと分かれば、それほど難しくはありませんが、グラフの意味を読み取る力も必要となってきます。
旅人算の基本をしっかり身につけてから取り組んでください。
旅人算とグラフとは
人算をグラフで表すと、2人の動きの様子が一目で分かります。グラフの縦軸は距離、横軸は時間を表し、2つの直線が交わる点がすれ違う(または追いつく)場所と時刻を示します。
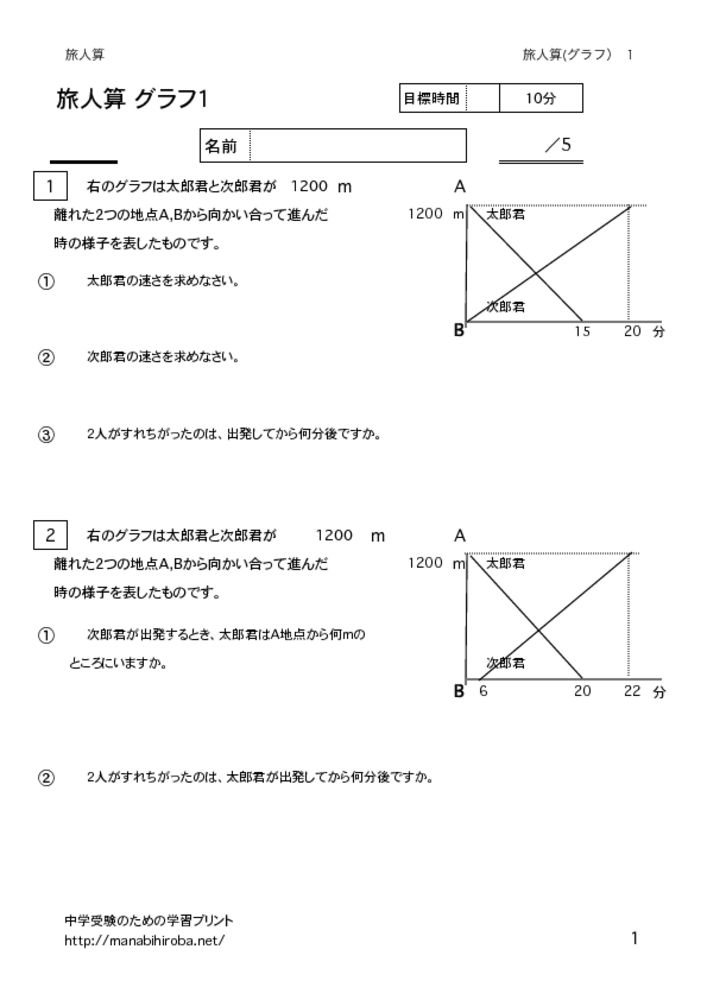
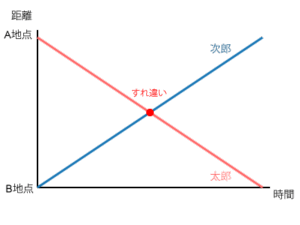
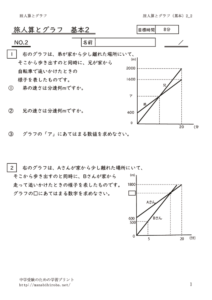
向かい合って進む旅人算のグラフ
2人がA地点とB地点から向かい合って出発する問題では、グラフは次のような形になります。
2つの線が交わる点が、すれ違った時刻と場所を表します。グラフから速さを読み取ったり、すれ違う時刻を計算したりする問題を練習しましょう。
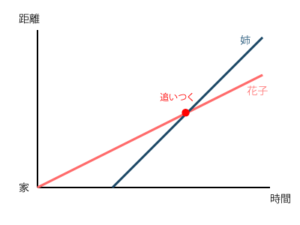
追いかける旅人算のグラフ
同じ方向に進み、後ろから追いかける問題では、グラフは次のようになります。
両方の線とも右上がりですが、速い方の線の傾きが急になります。2つの線が交わる点が、追いついた時刻と場所を表します。
学習のポイント
- グラフの傾きが急なほど速さが速いことを表します。グラフから2人の速さの関係を読み取りましょう。
- 向かい合って進む問題では、2人の速さを足すと「1分間にはなれる距離」が求められます。
- 追いかける問題では、2人の速さの差が「1分間に縮まる距離」になることを覚えておきましょう。
中学受験の速さの問題練習におすすめ
|
新品価格 |
 |
![]()
練習問題をダウンロードする
画像をクリックするとPDFをダウンロードできます。
*問題は追加する予定です。
出会いの問題
追いかけの問題
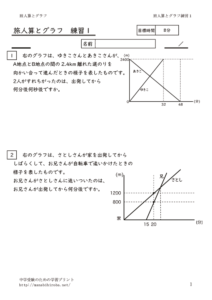
練習問題
基本問題より少し複雑な問題に挑戦できます。秒単位の計算や、往復する問題も含まれています。