通過算は速さの問題の中でも、図で理解しやすいので、いろいろな問題を解いて得意にしていきましょう。
速さや旅人算の基本がで出来ていれば解ける問題も多いので、基本的なことを確認して、得点源にするようにしてください。
通過算とは
通過算は、電車がトンネルや鉄橋を通過する問題です。電車には長さがあるため、電車の先頭がトンネルに入ってから最後尾が出るまでの距離や時間を考える必要があります。
学習のポイント
- 電車が進む距離は「電車の長さ+トンネル(鉄橋)の長さ」になる
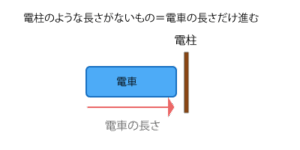
- 電柱や人など長さがないものを通過する場合は「電車の長さ」だけ進む
- 基本公式:距離=速さ×時間を使って計算する
通過算の基本
トンネルや鉄橋を通過する
トンネル電車電車の長さ+トンネルの長さ通過する=先頭が入ってから最後尾が出るまで 電車がトンネルを完全に通過するには、「電車の長さ+トンネルの長さ」の距離を進む必要があります。

例:長さ90mの電車が810mのトンネルを通過する → 電車が進む距離は 90+810=900m
電柱や人の前を通過する
電柱電車電車の長さ電柱のような長さがないもの=電車の長さだけ進む 電柱や人など、長さを考えなくてよいものの前を通過する場合は、「電車の長さ」だけ進みます。
例:長さ150mの電車が電柱の前を10秒で通過 → 150÷10=15より、秒速15m
列車がすれ違う・追いこす問題
2台の電車が関係する問題は、旅人算の考え方を使います。
すれ違う場合(向かい合って進む) → 2台の電車の長さの合計を、2台の速さの和で割る
追いこす場合(同じ向きに進む) → 2台の電車の長さの合計を、2台の速さの差で割る
学習のポイント
- 「通過する」とは先頭が入ってから最後尾が出るまでを意味します。距離の計算に注意しましょう。
- 時速と秒速の変換を忘れずに(時速を3600で割ると秒速になります)。
- 電柱や人など長さがないものを通過する場合は、電車の長さだけを考えます。
中学受験の速さの練習におすすめ

練習問題をダウンロードする
- 画像をクリックすると PDFファイルをダウンロードできます。
- 問題は追加予定です。
通過算 基本
通過算 練習
基本的な練習問題です。
通過算 いろいろな問題
やや複雑な内容を含む練習問題です。










