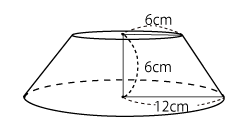相似比と体積比

立体の体積比の知識を使って、立体の体積などを求める問題です。

体積比を用いた方が、簡単に問題を解くことが出来ることもありますので、基本事項をしっかり確認してください。

体積比の基本

相似比が　a : b のとき、体積比は　(a×a×a) :（b×b×b）となります。

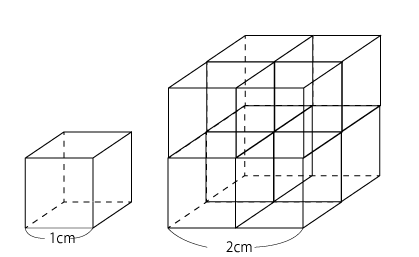
★ １辺が１cmの立方体と１辺が２cmの立方体では

相似比は　１：２　　体積比は　（１×１×１）：（２×２×２）＝１：8

円すいと体積比

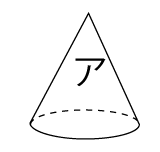
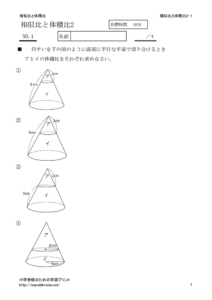
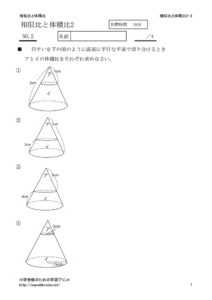
次のように円すいを底面に平行な平面で２つに分けたとき、アとイの部分の体積比を考えます。

小さい円すいア　と　大きい円すい（ア+イ）の　相似比は　　１：3　

ア　と　イ　の体積比は　　ア　：　｛（ア＋イ）　ー　ア｝　となるので

（１×１×１）：（3×3×3 ー１×１×１）＝１：26　　

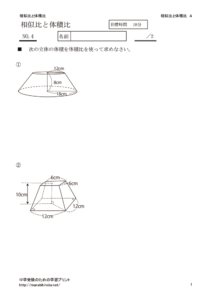
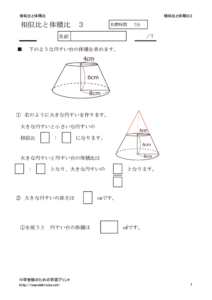
体積比を使って次のような円すい台の体積を求めます。

大きな円すいを作ると

大きな円すいと上の小さな円すいの相似比は　12：6＝2：1

大きな円すいと　円すい台の体積比は

（２×２×２）：（２×2×2ー１×１×１）＝8：7

円すい台の体積は全体の8分の7になる

円すい台の体積は　大きな円すいの体積×8分の7

円すいの高さは上の図より　①＝６cm  ②＝12cm で１２cmになるので

円すい台の体積は

12×12×3.14×12×1/3×7/8＝1582.56㎤　となる。

図形のまとめ学習におすすめ

中学入試 算数図形問題完全マスター 新品価格 ￥1,430から (2021/8/10 17:06時点)

練習問題をダウンロードする

画像をクリックするとPDFファイルをダウンロードできます。