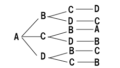
場合の数の中の道順が何通りあるかを求める問題です。
やり方が分かっていれば、解きやすい問題です。
基本的なことを理解して、確実に出来るようにしましょう。
道順の考え方
考え方を問われる問題も良く出題されるので、考え方からしっかり理解するようにして下さい。
下の図で、線をたどってAからBまで行く最短距離を考えます。

Bまで行く方法は 1+1=2通り になります。
今度は次の図を考えます。
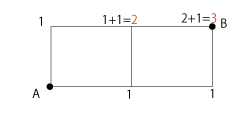
最初の角まで行くのが 1+1=2通り
次にBの角まで行くのが 2+1=3通りになります。
よってAからBまでの行き方は 3通りになります。
下の図でAからBまでの行き方は下のように計算できます;
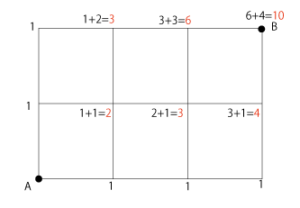
AからBの行き方は10通り
途中で通る道が決まっている場合
下の図で、AからBを通ってCまで行くときの最短距離を求める
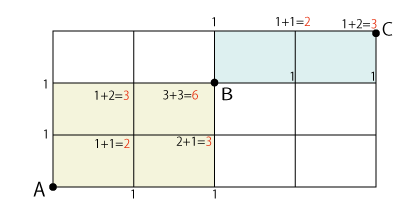
AからBまでとBからCまでの最短距離をそれぞれ求めると
AからBまで 6通り
BからCまで 3通り
よってAからCまでは 6×3=18通り
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロード出来ます。
問題は追加する予定です。
|
新品価格 |
 |
![]()