分配算・倍数算とは
分配算:全体の数量を複数の人に一定の条件で分ける問題
倍数算:「○倍」の関係がある2つの数量の問題
早ければ小学校2年生後半から取り組める、中学受験準備の基本レベルの問題です。中学受験の勉強を始めたばかりのお子さんでも取り組みやすい問題で、算数が苦手なお子さんも確実にマスターしてください。
基本的な考え方
例題1:倍数関係の分配算
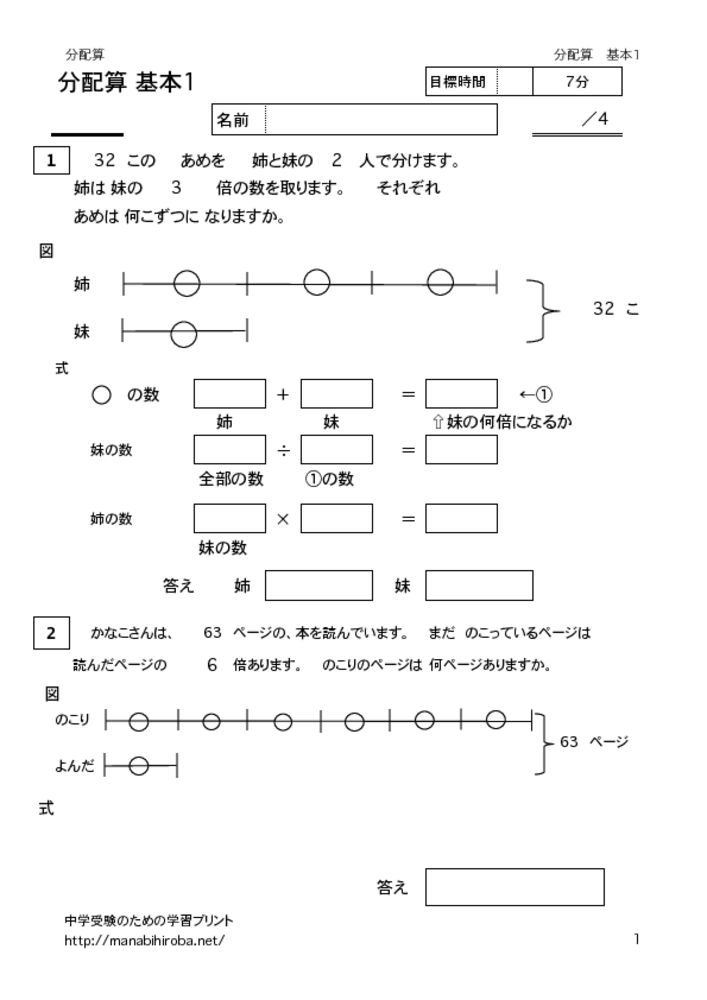
問題
28本のえんぴつを、兄と弟の2人で分けます。兄は弟の3倍の数を取ります。それぞれ何本ずつになりますか。
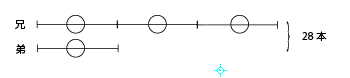
解き方 弟を○1つとすると、兄は○3つになります。
○の数:3+1=4
弟の数:28÷4=7本
兄の数:7×3=21本
答え:兄21本、弟7本
例題2:差の関係の分配算
問題
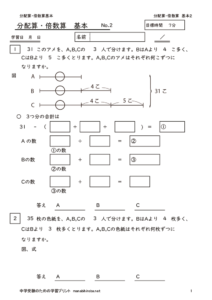
31個のアメを、A,B,Cの3人で分けます。BはAより4個多く、CはBより5個多く取ります。A,B,Cのアメはそれぞれ何個ずつになりますか。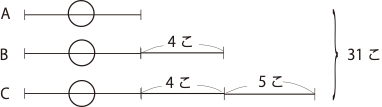
解き方 Aを○1つとします。
○3つ分の合計:31-(4+4+5)=18
Aの数:18÷3=6個
Bの数:6+4=10個
Cの数:10+5=15個
答え:A 6個、B 10個、C 15個
例題3:複合型の分配算
問題 41個のビー玉を、青と赤の2つのかごに分けます。青のかごは赤のかごの4倍より6個多く入れます。青のかごには何個入りますか。
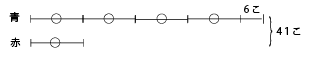
解き方 赤を○1つとします。
41-6=35
赤の数:35÷5=7個
青の数:7×4+6=34個
答え:34個
学習のポイント
- 線分図を正確に描く – 基準を○1つで表し、関係を図で表現
- 計算の順序 – ○の数→基準の数→各人の数の順で計算
- 答えが正しいか確認する – 合計が問題の数と一致するかチェックする
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロードできます。
基本的な考え方
基本練習問題
発展問題
基本レベルよりやや難しめの問題です