倍数算の問題です。
倍数関係にある2つの数量が、それぞれ増えたり減ったりした結果、最初とは違う倍数関係になるとき、初めの数量や結果の数量を求める問題です。
いろいろな問題が出題され、解き方も線分図で解く方法と比例式で解く方法があります。
問題によってやりやすい方法を身につけるようにしてください。
*線分図を使った基本的な倍数算の問題はこちら
基本的な考え方
線分図で解く方法
線分図を書く解き方は数量関係が目に見えてわかりやすいと思います。
線分図の書き方のパターンを確認して、いろいろな問題を解いてみるようにしてください。
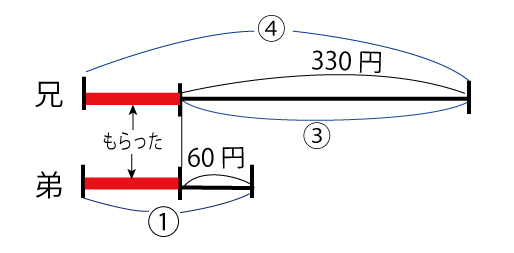
同じ数量が増えたり減ったりする場合
例題
兄は330円、弟は60円持っていました。2人とも同じ金額のおこづかいをもらったら兄の持っているお金は弟の4倍になりました。もらったおこづかいはいくらになりますか。
もらったお金が同じなので線分図を左にそろえて考える。
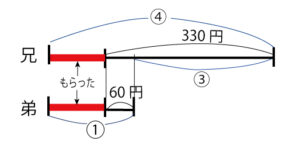
④−①=③ が 330-60=270円 なので
①=270÷3=90円 弟の方で考えると もらったお金は 90-60=30円 となる。
異なる数量が減る場合
例題
AとBは同じ金額のお金を持っていました。Aは100円、Bは400円使ったので、AとBの持っているお金の比は5:2になりました。はじめに持っていたお金はいくらになりますか。
減った部分の差を考える。
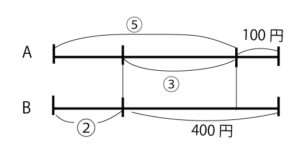
⑤−②=③ が 400-100=300円
①=300÷3=100円 Bの方で考えると 最初に持っていたお金は 100×2+400=600円 となる。
一方が増え、他方が減る場合
例題
兄と弟は同じ金額のお金を持っていました。その後、兄は200円もらい、弟は400円使ったので、兄の持っているお金は弟の3倍になりました。はじめに持っていたお金はいくらになりますか。
比の差の部分の合計を考える。
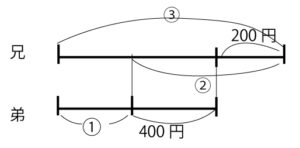
③−①=②が 200+400=600円 なので
①=600÷2=300円 弟の方で考えると最初に持っていたお金は 300+400=700円
学習のポイント
線分図をしっかり書いて、どの部分を求めるかを考えるようにしていきましょう。
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロード出来ます。
基本確認問題
練習問題
*問題は追加する予定です。
基本的な文章題の練習におすすめ
|
新品価格 |
 |
![]()