等差数列の基本
塾で公式を丸暗記してしまうケースが多いですが、なぜその式になるのかを理解することが大切です。
中学受験では、小学校で習う知識の範囲で考える必要があります。
等差数列とは?
となりあう数の差が一定の数列のことを言います。
例:
1, 4, 7, 10, 13, 16, 19…
(差はずっと「+3」で一定)
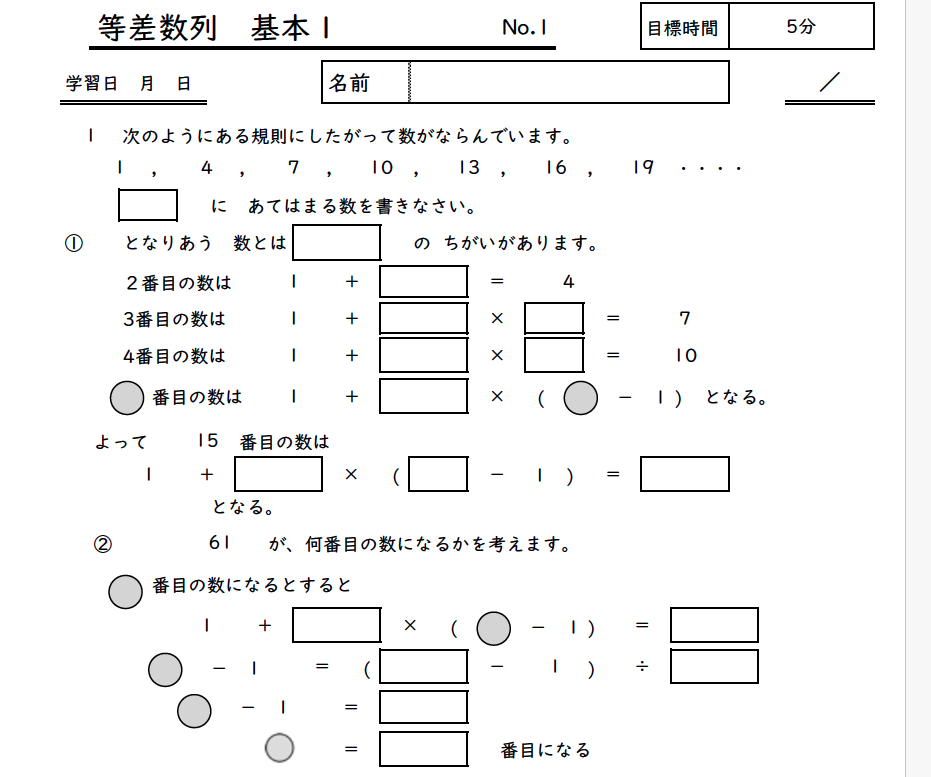
○番目の数の求め方
考え方
1番目の数に、差を「○−1回」足す。
【例題】 次のような数の並びがあります。
1, 4, 7, 10, 13…
この中で、15番目にあたる数を求めなさい。
式:1 + 3 × (15 – 1) = 1 + 3 × 14 = 1 + 42 = 43
答え:43
何番目かを求める方法
考え方
○番目の数の式を逆に考える。
【例題】
次のような数の並びがあります。
1, 4, 7, 10, 13…
この中に「61」という数があるとき、それは何番目の数かを求めなさい。
式:1 + 3 × (○ – 1) = 61
3 × (○ – 1) = 60
○ – 1 = 20
○ = 21
答え:21番目
数列の和(合計)の求め方
考え方
最初の数+最後の数をセットにすると、どれも同じ数になる!
【例題】
次の数列の和(合計)を求めなさい。
1, 4, 7, 10, 13, 16, 19
式:(1 + 19) × 7 ÷ 2 = 20 × 7 ÷ 2 = 140 ÷ 2 = 70
答え:70
あまりの数列も等差数列!
例
「5で割ると3余る数」
3, 8, 13, 18, 23, 28…
これも差が5の等差数列です。
○番目の数の式:
3 + 5 × (○ – 1)
一番小さい数の見つけ方
5で割ると3余る数で、最も小さい数を考えます。
0から順に調べてみましょう。
0 ÷ 5 = 0 あまり 0
1 ÷ 5 = 0 あまり 1
2 ÷ 5 = 0 あまり 2
3 ÷ 5 = 0 あまり 3 ← この数が条件に合います!
したがって、5で割ると3余る数のうち、一番小さい数は 3 です。
答え:3
あまりの数列での「何番目か」の求め方
【例題】
「5で割ると3余る数」の中に、「48」という数があります。この48は、何番目にあたる数でしょうか?
式:3 + 5 × (○ – 1) = 48
5 × (○ – 1) = 45
○ – 1 = 9
○ = 10
答え:10番目
まとめ
なぜそうなるのかを理解すれば、公式を覚えなくても自分で式を作って解けるようになります。
記述問題でも説明できるようにしておきましょう。
中学受験の算数の基本学習におすすめ
新品価格 |  |
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロードできます。
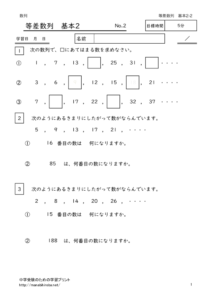
等差数列の基本
基本的な考え方と練習問題です。
*何番目の数を出す、数から何番目かを出す式を考えます。
等差数列の和
等差数列の和の基本的な求め方と練習問題です
あまりの数列
あまりの数列の問題です