いくつかのものから何個か選び出すと時の、選び方が何通りあるかを求めることを組み合わせといいます。
組み合わせの基本
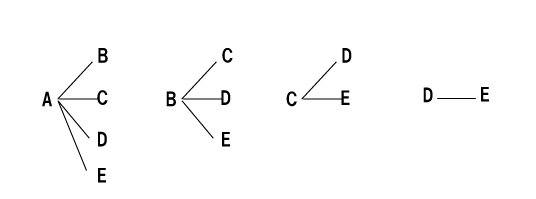
例）A,B,C,D,E の5人の中から2人ずつ組みになる作り方は何通りありますか。
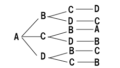
樹形図を書いて考える
並べ方と違って A-B 、B-A は同じ組み合わせになるので、重ならないように書いて考えます。
10通り
計算で考える
5×4＝20通り ←2人選ぶ並べ方
AB と BA は並べ方は違うが 組み合わせは同じになる。
20÷2＝10通り
最初のうちは図を書くのと計算を両方やって答えが同じになるか確認していくようにしましょう。
＊A,B,C,D,E の5人の中から3人ずつ組みになる作り方は何通りありますか。
→3人を選ぶと残りは2人なので 5人から2人の組を作るのと同じになる。
10通り
リーグ戦（総当たり戦）の問題
4つのチームが野球の試合を行います。どの試合も１試合ずつ対戦する時の試合数を求めます。
表を作って考えます。
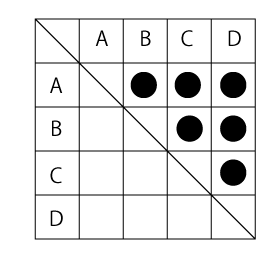
●が勝ちとすると全部で6試合と考えられます。
計算で考える
４つのチームから2チームの組み合わせで考えると
4×3÷２＝6 6試合 となります。
＊４チームがトーナメント戦をする場合
１チームずつ負けたチームが引かれていくので、試合数は4-1＝3試合となります。
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロード出来ます。
中学受験を成功させる 熊野孝哉の「場合の数」入試で差がつく５１題 ＋１３題改訂４版 (YELL books) 新品価格 |  |
