集合の考え方の問題です。
高校数学の集合でも使われる考え方ですが、集合で表した時の重なりなどの考え方が分かれば解きやすい問題が多いと思います。
問題文の読み取りも必要となりますので、問題の意味をしっかり理解して、表や図に表せるように練習してください。
表を作って考える
例)あるアパートに住んでいる40人について調べたら、大人が30人で、女性が24人だった。また、男性の子どもは4人だった。
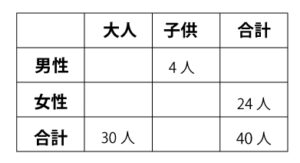
表の空欄を埋めていきます。
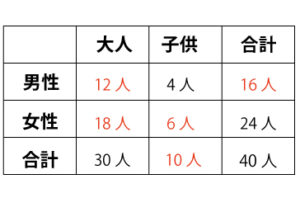
女性の大人の数、子どもの数などを求めることができます。
ベン図を書く
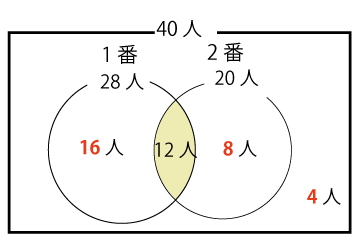
例)40人のクラスで算数のテストをしました。1番と2番の問題があって1番が出来た人が28人、2番が出来た人が20人、両方出来た人が12人でした。
この時、1番のみ出来た人、2番のみ出来た人、1番か2番の少なくとも一方が出来た人、両方とも出来なかった人の数を求めます。
*ベン図と呼ばれる図を書いて考えます。
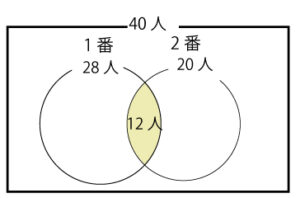
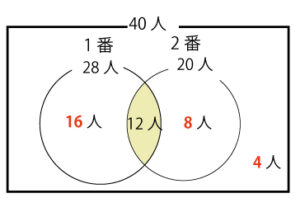
1番だけが出来た人の数
28-12=16 16人
2番だけが出来た人の数
20-12=8 8人
1番か2番の少なくとも一方ができた人の数
28+20−12=36 ←求め方を覚えておきましょう。
*上の1番だけ、2番だけが出来た人の数を使って16+12+8=36 と求めることも出来ます。
36人
両方とも出来なかった人の数
40-36=4 4人
*3つの集合を考える場合もあります。図を書いて考えるようにしてみてください。
*重なったところが0になる場合など、いろいろな集合を考えるようにしてみましょう。
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロードできます。
やや難しい問題も今後追加していく予定です。