回転体の体積、表面積を求める問題の解き方と練習問題です。
まずは、回転体をしっかりイメージする練習が大切になります。
下記のポイントから問題を解けるように練習してください。
学習のポイント
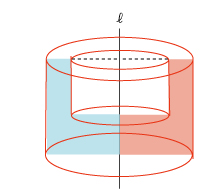
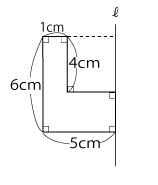
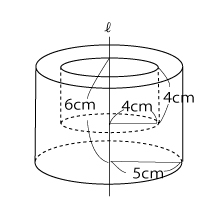
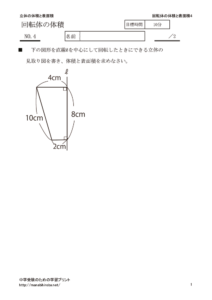
下の図形を直線ℓを中心にして回転したときにできる立体について考えます。
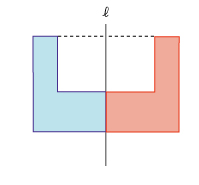
線対称の図形をかいてから、対応する２点を通る円をかく
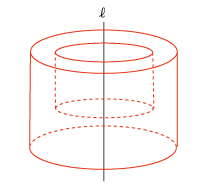
回転体の見取り図を書く練習から始めましょう。
まず、直線ℓに対して、線対称の図形をえがきます。
次に対応する２点を通る円をえがいていきます。
見えない部分を点にして完成です。
*いろいろな回転体を書いて練習しましょう。
くふうして体積や表面積を求める
上の回転体の体積と表面積を求めます。
円柱や円すいの体積、表面積を求める問題を解いてから取り組みましょう。
体積
（大きな円柱の体積）ー（小さな円柱の体積）で求められます。
5×5×3.14×6−4×4×3.14×4＝（150-64)×3.14＝270.04（㎤）
表面積
大きな円柱の側面＋小さな円柱の側面＋下の底面＋上の底面（ドーナツ型） の面積で求められます。
上の底面の面積はドーナツ型
5×5×3.14−4×4×3.14＝(25-16)×3.14=28.26 ㎠
大きな円柱の側面
5×2×3.14×6=188.4 ㎠
小さな円柱の側面
4×2×3.14×4=100.48 ㎠
下の底面の面積
5×5×3.14=78.5 ㎠
表面積は
188.4＋100.48＋78.5＋28.26＝395.64(㎠）
上は順番に面積を求めていますが、3.14以外のところをまとめてから計算するなど、計算方法はくふうしてみてください。
|
中学入試 分野別集中レッスン 算数 立体図形 (中学入試分野別集中レッスン) 新品価格 |
 |
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロードできます。
回転体を作図する問題
体積・表面積を求める
