つるかめ算とは
わからない2つの数量の合計ともう1つの条件から、それぞれの数量を求める問題です。
中学に入れば連立方程式で解ける問題ですが、小学校の知識だけで解いていくことになります。
6年生の後半になって文字式の理解が深まった段階で方程式を使うのもよいでしょう。ただし、中学受験では単純に方程式を作ればよいというものではなく、問題の意味をしっかり考えなければ解けない問題も多く出題されます。
方程式を作らないで頭で考えたほうが早い場合もあります。
まずは問題の意味をしっかり理解して、自分で解き方を考えられるようにしていきましょう。
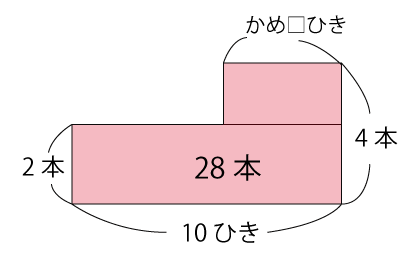
つるかめ算という名前の通り、鶴と亀の足の数から鶴と亀の数を求めるのが基本となります。
江戸時代の算数の問題にあったもので、中国の数学書にあった問題から考えられたようです。興味があったら江戸時代の算数(和算)についても調べてみてください。中学受験の算数の解き方の参考にもなります。
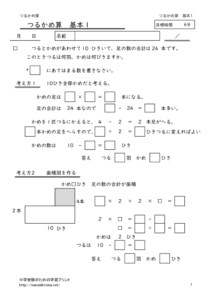
つるかめ算の基本的な考え方
例題)ツルとカメが合わせて10匹、足の数が合わせて28本のとき、ツルは何羽、カメは何匹いますか。ただしツルの足は2本、カメの足は4本です。

解き方1:すべて一方だと考える方法
10匹が全部カメだとします。
カメの足は 10×4=40本
カメの足を1匹ずつツルに変えていきます。

1匹ずつ変えるごとにカメの足は2本へります。
カメの足の数は 40-28=12本多いから
12÷2=6匹をツルにかえればよくなります。
よってツルは 6羽 カメは 10-6=4匹
解き方2:面積図で考える
面積図を書いて考えます。
たてが足の数、よこがツルとカメの数の合計となるように図を書きます。
ツルの数を先に求める場合。
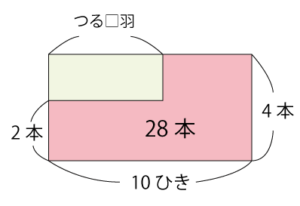
全体の面積から緑の面積をひくと28
10×4-2×□=28
□=(40−28)÷2=12÷2=6 ツルは6羽
カメの数を先に求める場合。
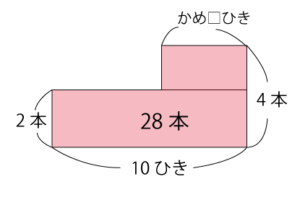
上と下の面積を足すと28
10×2+□×2=28
□=(28−20)÷2=8÷2=4 カメは4匹
求めた答えを確かめてみましょう
求めた答えを確かめてみましょう。ミスが少なくなります。
ツルは 6羽 カメは 4匹 と答えが出たから足の数の合計は
6×2+4×4=28 となり 問題の足の数の合計と同じになります。
つるかめ算の応用:弁償算
つるかめ算の考え方は、他の問題にも応用できます。
代表的なものが「弁償算」と呼ばれる問題です。
例題)1問正解すると5点もらえますが、間違うと2点引かれるクイズが20問あります。たかしさんは20問すべてに答えて、得点は72点でした。正解した問題は何問ありますか。
この問題も、つるかめ算と同じように考えることができます。
もし20問すべて正解したとすると、得点は5×20=100点
実際の得点(72点)との違いは、100−72=28点
正解を間違いに1問変えると、もらえる「5点」がなくなり、さらに「2点」引かれるので、合わせて7点減ることになります。
したがって、間違えた問題は 28÷7=4問
このように、「もらえるものと引かれるもの」がある問題も、つるかめ算の考え方で解くことができます。
*弁償算の詳しい解き方については、応用問題のプリントで練習してください。
中学受験の文章題の基本を学ぶのにおすすめ
|
中学受験 すらすら解ける魔法ワザ 算数・文章題 (西村則康先生の本) 新品価格 |
 |
![]()
練習問題をダウンロードする
*答えの求め方は解答と同じでなくても構いません。やりやすい方法で問題を解いてください。
*画像をクリックするとPDFファイルをダウンロードできます。
つるかめ算の基本
基本的な解き方を確認する問題です。
つるかめ算の練習問題
基本的な練習問題です。
応用問題(弁償算)
基本的な弁償算の解き方の問題です。