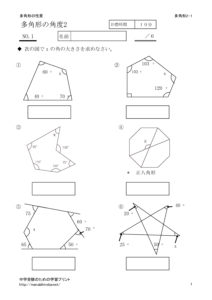
多角形の内角の和と対角線の数の問題です。
公式を覚えておけば出来ますが、最近は公式の導き方を問うことも増えています。
丸暗記するのではなく、多角形の性質をしっかり確認して公式を使うようにしていきましょう。
多角形の内角の和
六角形の内角の和を求める場合

上のように4つの三角形に分けられるので、三角形の内角の和は180°だから
六角形の内角の和は 180×4=720° となる。
n角形の内角の和=180×(n-2)
多角形の外角の和
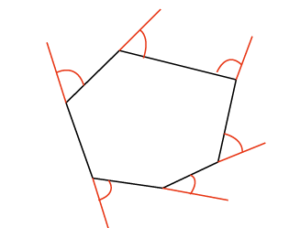
多角形の外角の和はつねに360°
多角形の対角線の数
六角形の対角線の数を考える

1つの頂点からひける対角線は 3本
*頂点自身と、両怒鳴りの頂点には引くことはできない
式にすると 6-3

6つの頂点からひける対角線は 3×6=18本
どの対角線についても1本の対角線を2回づつ数えることになるのでこれを2で割らなければならない。
18÷2=9本
1つの式でまとめると (6−3)×6÷2=9本
n角形の対角線の数=n×(n-3)÷2
*公式をそのまま覚えていると忘れやすいので、上の求め方を確認しておきましょう。
練習問題をダウンロード
画像をクリックするとPDFファイルをダウンロードできます。
問題は追加する予定です。