中学受験の割合の応答問題としてよく出題される売買算の基本です。
物の売り買いでの原価(仕入れ値)、定価、売値に関する利益を考える問題です。
いろいろな応用問題が出題されますが、基本的なことをしっかり出来るようにしてから応用問題を解くようにして下さい。
基本的な用語の意味をしっかり確認する
言葉の意味が分からないないと問題は解けません。
原価(仕入れ値)、定価、売値、利益の意味をまずは確認して下さい。
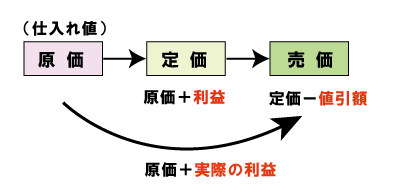
お店が仕入れた値段が原価
定価は原価+見込まれる利益
売値 実際に売る値段 (定価ー値引きした値段)
実際の利益=売値ー原価
実際に買い物に行って割引されている商品があったら、いくら割引されるかお子さんと一緒に考えてみるようにしましょう。
割増しと割引きの計算をしっかり出来るようにする
基本的な割増し、割引きの問題を確実に出来るようにしてから、いろいろな問題をとるようにして下さい。
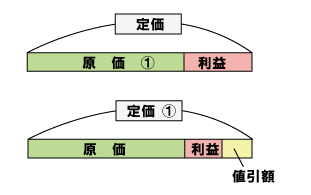
割増しの場合原価を1と考える
例)原価500円の品物に2割の利益を見込んで定価をつける。
2割=0.2
500×0.2=100 円 が利益になるので 500+100=600(円)と求めても構いませんが、複雑な問題になると数直線で一度に考えていかないと解きづらくなってきます。
原価を1と考えて 定価は(1+0.2)になるから 原価の(1+0.2)倍が定価になるという考え方を身につけるようにしましょう。
500×(1+0.2)=500×1.2=600円
定価=原価×(1+利益)
割引きの場合定価を1と考える
例)原価600円の品物を2割引で売る
こちらも割引した値段が 600×0.2=120円
なので 600-120=480円と求められますが
定価を1と考えると 売値は(1-0.2)になるので 定価の(1-0.2)倍が売値になると考えます。
600×(1−0.2)=600×0.8=480円
売値=定価×(1ー割引率)
複雑な問題は順番に考えていく
複雑な問題は順番に考えていきましょう。
例)定価2000園の品物に2割の利益を見込んで定価をつけましたが、売れないので1割引きにしました。売値はいくらになりますか。
定価を求める
2000×(1+0.2)=2400(円)
売値を求める
2400×(1-0.1)=2160(円) 答え 2160円
入試では利益から売った個数を求める問題など、さらに複雑なものも出題されますが、基本がしっかりできれば少しずつ解けるようになります。
まずは基本的な問題を短時間にできるようにして下さい。
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロードできます。
割り増し、割り引きの問題
割り増し、割り引きの計算練習です。
売買算の問題
問題文を読んで順番に考えていきます。分かりづらい場合は、線分図などを書いて考えてください。
割合の問題の基礎がためにおすすめ
|
新品価格 |
 |
![]()







